Problem 1: Cash Money

In the game of roulette, players bet on the outcome of a ball randomly landing in 38 distinct slots labeled with the numbers \(1\)–\(36\), \(0\), and \(00\). The numbers in the range \(1\)–\(36\) are furthermore colored as follows: \[\begin{align*} 1, 3, 5, 7, 9, 12, 14, 16, 18, 19, 21, 23, 25, 27, 30, 32, 34, 36 &= \mathsf{red} \\ 2, 4, 6, 8, 10, 11, 13, 15, 17, 20, 22, 24, 26, 28, 29, 31, 33, 35 &= \mathsf{black} \end{align*}\] Give combinational descriptions (i.e., unsimplified formulae) for each of the required values.

1. What is the probability of winning a “00” bet (where the ball lands on \(00\))?
2. What is the probability of winning an “odd” bet (where the ball lands on an odd number)?
3. What is the probability of winning either a “1st dozen” bet (where the ball lands on a number in the range 1–12) or a red bet (where the ball lands on a red number)?
4. What is the probability of winning both an “even” bet (where the ball lands on an even number, 0 and 00 do not count as even) and a “3rd dozen” bet (where the ball lands on a 25–36)?
5. Let \(X\) be a random variable describing the pay-off of a single set of bets in dollars. What is the expected value of placing both a “black” bet (where the ball lands on a black number) and a “1st dozen bet” bet if the pay-off for the black bet is 1 dollar and the pay-off for the “1st dozen bet” is 2 dollars?

Problem 2: Being John Markovian

Frequently, we can view a computation as a system moving through a series of states. For example, consider modeling a student’s behavior during a day of school. For simplicity’s sake, we’ll consider two states:

• The student is in bed.
• The student is in class.

When in bed, the student can either stay in bed or head out to class. Likewise, when in class, the student can either stay in class or head back to bed. This system can be modeled as a directed graph where nodes are states and edges between states \(s_1\) and \(s_2\) imply that the system is capable of moving from state \(s_1\) to state \(s_2\). Our example is modeled by the following directed graph:

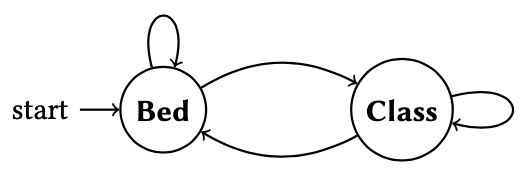
For example, the graph tells us that if the student is in bed, then they may either transition to class \((\mathsf{Bed}, \mathsf{Class})\) or stay in bed \((\mathsf{Bed}, \mathsf{Bed})\). Generally, this model is called a finite automata—a finite collection of states with rules describing how the system can transition between states.

From this graph, it appears that a student is equally likely to go to class or to stay in bed when they are already in bed. However, we all know this is not the case! To model the fact that it is more likely to stay in bed than go to class, we’ll introduce __robabilities_ to the transitions denoting how likely it is a student will move from one state to another. For example, we might note that:

\[\begin{align} p( \mathsf{Bed}, \mathsf{Class} ) =&\; \frac{1}{10} \\ p( \mathsf{Bed}, \mathsf{Bed} ) =&\; \frac{9}{10} \\ p( \mathsf{Class}, \mathsf{Class} ) =&\; \frac{1}{2} \\ p( \mathsf{Class}, \mathsf{Bed} ) =&\; \frac{1}{2} \end{align}\]

This results in the following modified graph:

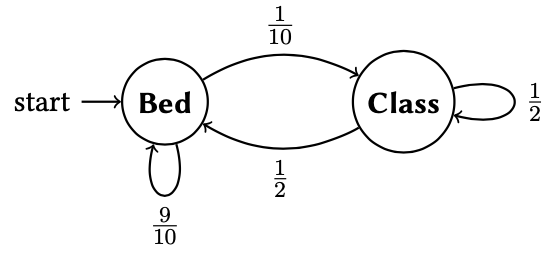
We call this modified graph a Markov chain, a probabilistic finite automata.

1. Consider an arbitrary node \(s \in V\) of a Markov chain. Give a formula relating the sum of all the probabilities of the transitions out going from \(s\). In other words, what value is this summation equal to (where \(s\) is fixed to a particular node and \(s'\) is any node that \(s\) is connected to via an edge):

   \[ \sum_{(s, s') \in E} p(s, s')? \]

   Explain your answer in a few sentences, making sure to appeal to the relevant properties of the probability mass function.

2. To model our system evolving over time, we will use a sequence of random variables \(X_1, \ldots, X_t\) representing the state of the system at time steps \(1\) through \(t\), respectively. A probability distribution \(\Pr(X_t = s_t)\) denotes the probability that the system is in state \(s_t\) at time \(t\). For example the random variable \(X_1\) corresponds to the initial state where:

   \[ \Pr(X_1 = s) = \begin{cases} 1 & s = s_0 \\ 0 & \text{otherwise} \end{cases} \]

   And \(s_0\) is the initial state of the Markov chain.

   Any Markov chain respects the Markov Property which states the following:

   \[ \Pr(X_{k+1} = s \mid X_1 = s_1, \ldots, X_k = s_k) = Pr(X_{k+1} = s \mid X_k = s_k). \]

   Recall that conditional probability of event \(A\) given \(B\), written \(P(A \mid B)\) is the probability of \(A\) occurring assuming that \(B\) has already occurred. Give an informal description of the Markov Property in a few sentences.

3. Consider our bed-class example above. In a few sentences, describe what does the Markov Property says about the probabilities of transitioning between bed and class?

4. In a few sentences, describe how we could change our bed-class example so that it does not obey the Markov Property. (In other words, what additional consideration could we make about the probabilities that would violate the Markov Property?)

5. Finally, we’ll derive a recurrence relation describing the probability distribution of the sequence of random variables \(X_1, \ldots X_t\) describing the likelihood that we’re in a particular state at a given time step in our bed-class example. A recurrence relation is a set of recursive equations; here, we will describe the probability distribution of the random variables by recursion on the time step \(t\).

   First, fill out the base case of the recurrence. Let \(Pr(X_1 = s)\) be the probability that the system is initially in state \(s\) where \(s \in \{ \mathsf{bed}, \mathsf{class} \}\). Give values for both \(\Pr(X_1 = \mathsf{bed})\) and \(\Pr(X_1 = \mathsf{class})\). (Hint: what states can we be in initially?).

6. Next, fill out this table capturing the next four cases of the recurrence through \(X_5\).

   Time	\(X_t = \textsf{bed}\)	\(X_t = \textsf{class}\)
   \(t = 1\)	(from (5))	(from (5))
   \(t = 2\)
   \(t = 3\)
   \(t = 4\)
   \(t = 5\)

   (Hint: according to the Markov Property, what does the probability of a given state \(s\) and time \(t\) depend on?)

7. Finally complete the recurrence by writing out its recursive case \(\Pr(X_{k+1} = s_{k+1})\) in terms of the probability distribution of \(\Pr(X_k = s_k)\). The recursive case should generalize the computation you used to fill out the table above. You do not need to prove that recurrence is correct.

8. Use the recurrence relation to estimate the probability that the system is in each possible state—\(\mathsf{bed}\) and \(\mathsf{class}\)—as the number of time steps grow very large.