Problem: Minimum Spanners
Consider the following weighted, undirected graph:
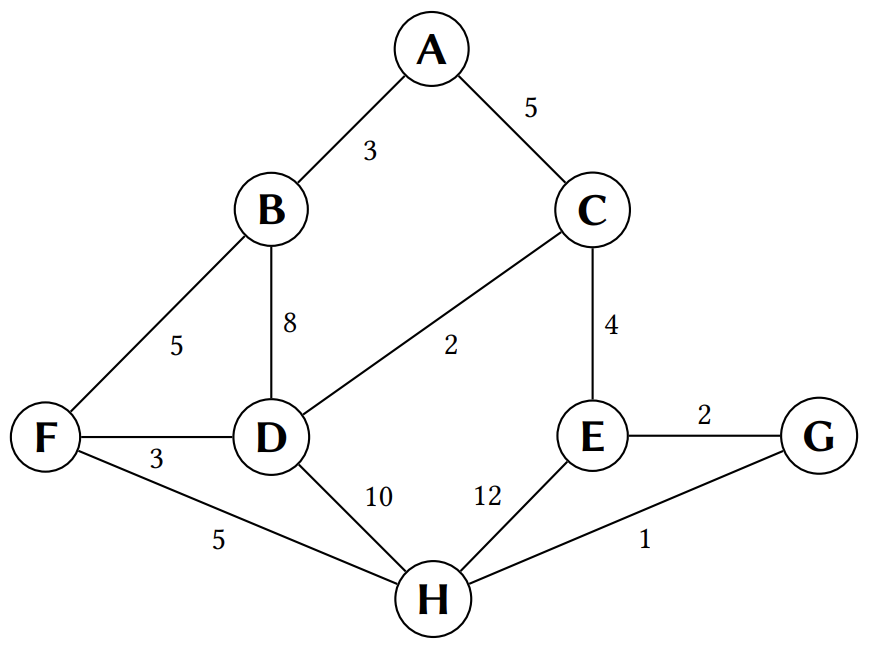
Come up with at least three spanning trees for this graph using the techniques discussed in the reading. Write down the collection of edges that compromises each tree.
When our graphs have weights, we are concerned with finding minimum spanning trees (MSTs), spanning trees whose sum-of-weights-of-edges is minimal for any spanning tree of the graph. Come up with a MST for this graph. Note that:
- A naive breadth-first or depth-first search will not necessarily find a MST, so you will likely need to use guess-and-check to find the answer.
- There may be more than one MST, but the weight of all such MSTs should be equal.
Note the edges of your MST and the sum-of-weights of that tree. Check with an instructor that your MST is indeed the minimal one.
Now we will spend the rest of the time deriving an algorithm for finding a MST of a given graph. First spend some time with your partner to brainstorm ways that you might change your traversal algorithms to account for the weights of the edges. Do not just the candidate algorithms that your group proposes—they’ll likely have flaws! Merely note them in your write-up. Try to come up with at least two distinct attempts at an algorithm.
Consider the following prompt for a potential algorithm:
Start with a MST of one node and then grow the MST incrementally from there.
Develop an algorithm to find a MST based on this prompt. I highly recommend playing with the graph above or coming up with your own examples to try out ideas. Write down your final candidate algorithm in your write-up as well as a brief reason why the algorithm is correct (not necessarily a proof although you are welcome to do so if you have time).